|
| | Fabriquez vous -meme votre simulateur de compteur nucléaire |  |
|
+9Gally Iron Kloug Thorvald Samael22 Domino Toz Seba Kokura Marie M. 13 participants | |
| Auteur | Message |
|---|
daima
Acrobate

 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 11:36 Ven 9 Aoû 2019 - 11:36 | |
| Bonjour cher Gluonmou, Pas flashman mais le boulot de RP nécessite souvent de maitriser des tableaux complexes pour toute sorte de tâche et quand une formule marche pour deux colonnes, pas dur de la refaire pour 10. - Citation :
- Allez, une petite indication : pensez à la probabilité pour qu'une valeur de la somme pousse très proche de 0 , c'est plus facile pour amorcer la réponse
En logique pure, on a des chances infimes qu'elle soit proche de 0 pour chaque série d'alea(), la probabilité que la coincidence que les deux alea() soit proche de 0 en même temps est quasiment improbable. Cette logique est applicable de la même manière pour les valeurs proches de 2. Alors qu'obtenir une valeur de 1 est plus simple avec la somme de deux alea(), il y a plus de combinaison possible 0+1, 0,1+0,9, ... 0,5+0,5. Intuitivement ça se comprend bien. A l'écrire, j'ai pas les notions. |
|   | | Gluonmou
Contorsionniste

 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 12:03 Ven 9 Aoû 2019 - 12:03 | |
| Bravo, c'est exactement cela, une histoire de nombre de combinaisons possibles pour obtenir un résultat donné. (et vous meritez bien votre prénom de flashman)
Une combinaison quelconque par exemple (U1=0,28 et U2=0,42) a autant de chance d’apparaître que n'importe quelle autre combinaison, genre U2=0,37 et U2=0,75
Pour obtenir U1+U2=0 il n'y a qu'une combinaison possible : U1=0 et U2=0
Idem pour U1+U2=2 (le max) il n'y a qu'une combinaison possible : U1=1 et U2=1
Alors que pour obtenir la valeur centrale U1+U2=1 il existe un très grand nombre de combinaisons possibles :
toutes les combinaisons de la forme U1=x et U2=1-x (par exemple U1=0,1 et U2=0,9 ou U1=0,2 et U2=0,8 etc...)
nota : dans l'expression x et 1- x on voit apparaître un outil fondamental dans la gestion des distribution : le concept de produit de convolution
Donc la valeur somme U1+U2=1 est très probable, et par raison de symétrie c'est même la plus probable
Il est donc normal que la distribution parte de 0, passe par un maximum à 1 et retombe à 0 pour Y=2
Cette histoire de nombre de combinaisons possibles pour obtenir un état final est l'un des piliers de la physique. En physique statistique, domaine hélas mal connu (Einstein était un physicien statisticien, à ne pas confondre avec un gars qui bosse à l'INSEE) le nombre s'appelle du joli nom de "nombre de complexion W et apparaît dans la relation tout autant fondamentale que célèbre de l'entropie au sens de Boltzmann :
S=k log(W)
Relation par ailleurs écrite sur sa tombe.
Gluonmou
PS : vous voyez qu'il y a beaucoup de chose à dire autour de notre petite simulation indispensable |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 12:08 Ven 9 Aoû 2019 - 12:08 | |
| Je fait e point dans l'avancement du cours
la question en suspens est maintenant
A quoi commence à ressembler la somme de 10 alea
là encore il y aura u un truc fondamental
Je rajoute une question subsidiaire
Après avoir fait la somme des 10 alea, faites en la moyenne (soit la somme divisée par 10)
faites ça dans la même colonne, histoire de garder le même histogramme (il est par contre utile de redéfinir l'échelle de l'histogramme, le min et le max
On va arriver à l'un des théorèmes les plus puissant et intéressant, en termes d'applications pratiques (métrologie, incertitude..) des statistiques |
|   | | Domino
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 16:42 Ven 9 Aoû 2019 - 16:42 | |
| Bon, suis un peu perdue et mes incompétences en matière Excel n'arrange rien. 1. pas moyen de faire les histogramme par fréquence ce qui explique l'absence de bosse ou de triangle dans mon graphique 2. pour la moyenne des 10 alea, j'ai du louper un truc: je trouve 5 pour la somme des 10 alea ce qui me parait logique. Si je divise par 10, je retrouve la moyenne par alea soit 0,5 
_________________
l' ouverture d'esprit n'est pas une fracture du crâne
Dernière édition par Domino le Ven 9 Aoû 2019 - 17:27, édité 1 fois |
|   | | Iron Kloug
Homme-canon


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 17:16 Ven 9 Aoû 2019 - 17:16 | |
| Bonjour
J'en suis au plus bas niveau pour le tableur excel... Tu es même certainement bien plus évoluée que moi.
Iron Kloug _________________ Show must go on !  |
|   | | Domino
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 17:29 Ven 9 Aoû 2019 - 17:29 | |
| Merci Kloug, contente de ne pas être la seule 
_________________
l' ouverture d'esprit n'est pas une fracture du crâne
|
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 19:32 Ven 9 Aoû 2019 - 19:32 | |
| Si vous saviez tout ce que l'on peut faire avec Excel, vous en rougiriez!
C'est hélas devenu le symbole d'un management qui part en cacahuette
par contre c'est pas évident d'expliquer comment on utilise la fonction frequence
C'est fastoch à montrer devant un ordi, mais là juste avec une machine à écrire
Un volontaire pour le faire?
Bon,sinon on va attendre un peu les retardataires pour discuter autour de la somme et de la moyenne de 10 alea, puis on reviendra au jeu depile ou face..
Le compteur nucléaire n'est plus trop loin
Gluonmou |
|   | | Domino
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 22:26 Ven 9 Aoû 2019 - 22:26 | |
| Ouf!une courbe!  La moyenne de chaque ligne permet d'affiner les données et d'avoir une courbe centré sur la moyenne de 0,5 (le pile ou face étant le postulat de départ) (merci pour le cours Excel)
_________________
l' ouverture d'esprit n'est pas une fracture du crâne
|
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Ven 9 Aoû 2019 - 23:06 Ven 9 Aoû 2019 - 23:06 | |
| Bon, maintenant que Domino a réglé ce petit problème de fréquence (en fait d'effectif), on va avancer un peu Ci dessous la distribution de la somme de 15 alea Au passage ce nombre 15 s'appelle taille de l'échantillon, je le noterai toujours n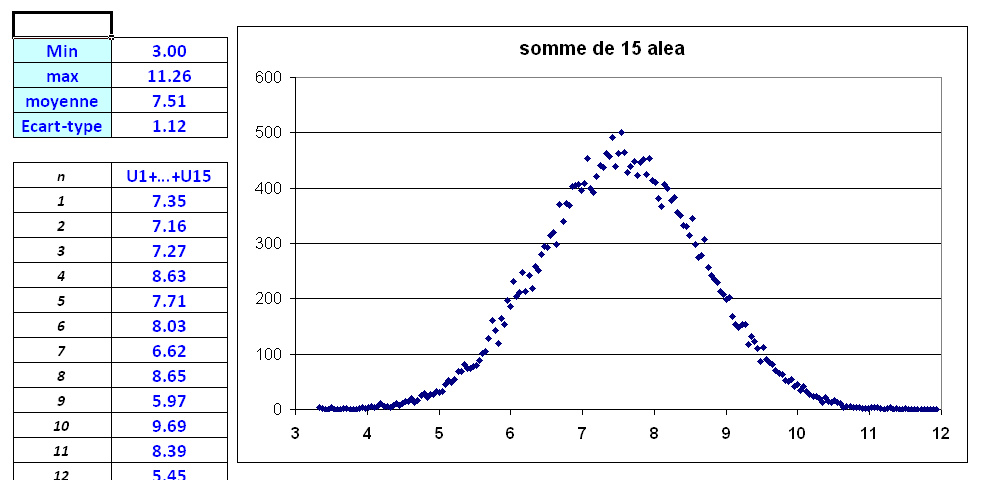 On constate que cette distribution commence à ressembler à une gaussienne Et là on retrouve le théorème central limite (TCL), qui nous dit qu'effectivement lorsque la taille l'échantillon n tend vers l'infini, la somme tend vers une gaussienne. balèze, non? Vous ajoutez plein de trucs non gaussien, et de loin et vous obtenez une gaussienne. Le TCL montre que ça marche avec n'importe quelle VA de départ Au passage cet exemple est une première méthode pour construire une VA gaussienne acceptable partir du random (je rappelle ici que le terme random s'applique ici à la VA continue uniforme entre 0 et 1, sous VBA il s'écrit rnd()) . On conseille en général de prendre au moins n=12 Q1) La simu montre que l'écart-type pour n=15 , en appuyant plusieurs fois sur f9, varie en gros entre 1,11 et 1,13 . (on notera au passage que cet écart-type est lui aussi une variable aléatoire). Quelle est sa valeur exacte? on appliquera ici la relation sur la variance de la sommeQ2) même question pour la moyenne de n aléa (n=10 ou 15, comme vous voulez. Quelle est la relation entre l'écart-type de alea et l'écart-type de la moyenneCi-dessous sa distribution et l'estimation de ses paramètres (moyenne, ecart-type etc) Ou l'on constate que la moyenne d'un échantillon de 15 valeurs fluctue moins que la variable de départ, c'est à dire se resserre autour de sa moyenne vraie, ici 0,5 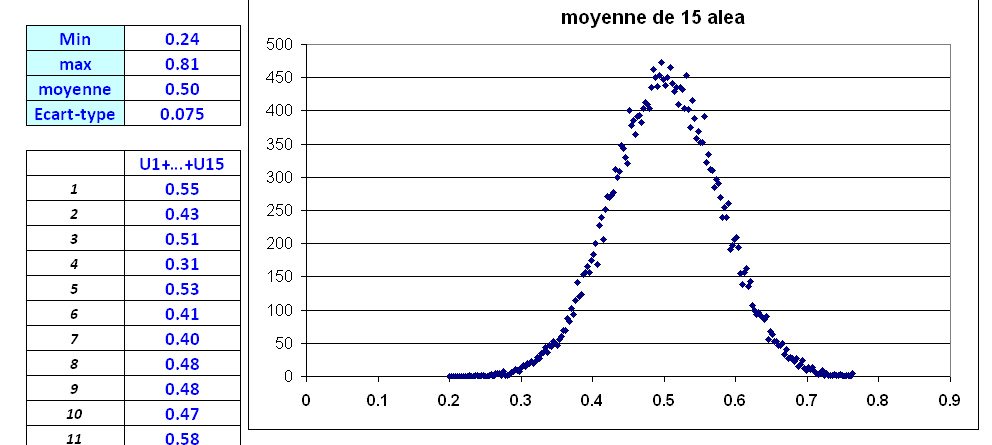 |
|   | | Domino
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Sam 10 Aoû 2019 - 12:26 Sam 10 Aoû 2019 - 12:26 | |
| Pour la question 1: j'ai 1,109 (racine de la variance de la somme)
Pour la question 2: l'écart type de la moyenne est l'écart type de la somme/n
_________________
l' ouverture d'esprit n'est pas une fracture du crâne
|
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Sam 10 Aoû 2019 - 13:12 Sam 10 Aoû 2019 - 13:12 | |
| OK mais arrétons nous un peu sur ce résultat La moyenne se construit comme la somme de n VA , somme divisée ensuite par n Du coup on pourrait penser que l'écart-type de la moyenne est celle de l'aléa de base (en algébre x+x+...x n fois =nx puis divisé par n on retrouve x) Ben avec les VA indépendantes ça ne marche pas comme ça Var(U1+U2+..+Un)=Var(U1)+Var(U2)+...Var(Un)=n Var(U) (=0,29) Mais rappelez vous que Var (aX)=a^2Var(X) Donc Var(moyenne)=Var([U1+U2+..+Un]*1/n)=1/n^2Var(U1+U2+..+Un)=n/n^2 Var(U)=1/n Var(U) Soit en revenant à l'écart-type :  (moenne de taille n)=1/racine(n)  (U) La variable moyenne d'un échantillon de taille n, car c'est bien aussi une variable aléatoire est divisé par racine (n) par rapport à l'écart-type "de base" Propriété puissante : plus n augmente,moins la moyenne fluctue, ce qui veut dire qu'une moyenne expérimentale est de plus en plus proche de la moyenne vraie. Nous y reviendrons Je vais maintenant revenir après ce long détour à notre simulation de pile ou faceNous avons construit dans une cellule le nombre de succès(face) pour un jeté de 1000 pièces, soit une grandeur entière "tournant" autour de 500 (grandeur moyenne légitimement "attendue) Ce compteur, lorsque l'on appuis sur f9, se comporte comme une variable aléatoire C'est une variable aléatoire, au demeurant c'est même a fameuse variable binomiale, dont la variable est une grandeur entière positive et la loi la fameuse loi binomiale qui vous a donné des cauchemars à l'école C'est une loi à deux paramètres : n (pour nous ici n=1000) et p Q1) Si l'on se rappelle que l'on a construit cette VA binomiale comme la somme de n épreuves de Bernoull de paramètre p, quel est alors l'écart-type de cette variable Q2) Comment écrire alors la valeur moyenne attendue (vrai) et l'écart-type vrai (cf Q1) en fonction des 2 paramètres n et p le compteur nucléaire se rapproche Gluonmou PS : y'a plus que Domino qui suit? |
|   | | Domino
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Sam 10 Aoû 2019 - 20:00 Sam 10 Aoû 2019 - 20:00 | |
| Q1: c'est ce qu'on avait fait au début avec la variable alea? Ecart type 0,29? avec une moyenne à O,5
Q2: moyenne vrai pour n=1000: 500= n x p
Ecart type vrai: racine n x p x (1-p): 15,39
Du coup, la moyenne expérimentale se rapproche de la valeur théorique mais l'écart-type pas vraiment.
J'ai du foiré un truc???
_________________
l' ouverture d'esprit n'est pas une fracture du crâne
|
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Sam 10 Aoû 2019 - 23:13 Sam 10 Aoû 2019 - 23:13 | |
| "Q1: c'est ce qu'on avait fait au début avec la variable alea? Ecart type 0,29? avec une moyenne à O,5"
Il faut oublier la variable alea
ici nous avons fabriqué 1000 épreuves de Bernouilli : 0 ou 1
Puis nous avons sommé les résultats des 1000 épreuves pour avoir le nombre total de sucés (face)
C'est ça notre variable aléatoire binomiale
nous avions montré que l'écart-type d'une épreuve de Bernouill était racine(p*(1-p))
Donc l'écart-type de n épreuves de bernouilli est égal à : racine(np*(1-p))
Q2) les paramètres de la loi de probabilité d'une VA binomiale sont n et p (resp. 1000 et 0,5 ici)
A partir de ces 2 paramètres on peut calculer :
- la moyenne (espérance) vraie : µ=n*p . Dans notre exemple np=500 (le nombre de face attendu
- l'écart-type vraie = racine(np*(1-p)=50
Bon, il est temps d'aborder l'avant dernier chapitre : le compteur nucléaire
ben c'est assez simple : on va refaire comme pour le jetés de 100 pièces mais avec quelques modifs :
1) on va prendre (pour commencer) 10 000 épreuves de Bernouilli au lieu de 1000
2) on va prendre p=0,0025 au lieu de 0,5
3) et on refait la somme des 10 000 épreuves, qui devient notre compteur
Q1) calculer les paramètres vraies de cette variable
Q2) donnez une estimation expérimentale en répétant le comptage et comparez
Q3) pourquoi peut-on penser que l'on tient enfin une variable qui ressemble effectivement à une "variable de Poisson"
Si vous regardez de près, c'est assez facile à construire
Mais on aura encore 2 ou 3 petites choses à voir après
Gluonmou |
|   | | Domino
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Dim 11 Aoû 2019 - 11:25 Dim 11 Aoû 2019 - 11:25 | |
| Bon, puique j'ai commencé, allons jusqu'au bout.
Pour l'avant dernière question avec p=0,5 et n=1000
J'avais un écart type de 15,39
Tu dis qu'il est de 50
Ne serais-ce pas pour n=10000 qu'il est de 50?
Sinon pour n=10000 et p=0,0025
la moyenne est de 25 et l'écart type de 4,99 soit la racine carrée de la moyenne
Et donc, la pêche est bonne et j'ai un poisson
Moralité:avant de choisir une formule, savoir à quelle type de population on s'adresse au risque de se noyer
_________________
l' ouverture d'esprit n'est pas une fracture du crâne
|
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Dim 11 Aoû 2019 - 15:35 Dim 11 Aoû 2019 - 15:35 | |
| Oui, effectivement , pour n=1000 et p =0,5 l'écart-type est égal à 15,..
50, ça me paraissait effectivement beaucoup, même pour une variable binomiale
je me mélange un peu les crayon entre mes colonnes de 1000 valeurs et de 10 000
Pour construire le compteur nucléaire il faut bien prendre n=10 000, c'est un minimum
Un milliard, ce serait mieux
Gluonmou |
|   | | Domino
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Dim 11 Aoû 2019 - 15:54 Dim 11 Aoû 2019 - 15:54 | |
| Quand je parle de population, c'est surtout savoir dans quel cas de figure on se trouve.
J'aime bien le chemin parcouru pour passer de la binomiale à la loi de Poisson.
Le corollaire( important) étant qu'on ne peut par dire que l'écart type est la racine de la moyenne dans n'importe quelle situation.
_________________
l' ouverture d'esprit n'est pas une fracture du crâne
|
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Dim 11 Aoû 2019 - 19:28 Dim 11 Aoû 2019 - 19:28 | |
| LE COMPTEUR NUCLEAIRE SOUS EXCEL Gratos et sans sourceEn résumé, si vous voulez passer directement à l'application, il faut commencer par faire une grande colonne de n épreuves de Bernouilli "Ent(alea()+ p)"  En respectant les conditions suivantes : n grand (10000 min) et p petit (max 1/100) En sommant les n épreuves vous obtenez une variable N entière qui suit une loi de Poisson (voir image) dont la caractéristique essentielle est d'être une loi à un seul paramètre µ=n*pµ est la moyenne vraie de la distribution de Poisson C'est une grandeur qui peut prendre des valeurs quelconques, non entières, entre 0 et + l'infini Dans le modèle de la mesure nucléaire, on peut relier N à une activité mesurée, opération que l'on peut répéter avec des résultats différents Dans le même modèle ( à condition de connaitre le rendement vraie qui est en fait expérimentalement lui aussi une variable aléatoire) on peut relier µ à l 'activité vraie contenue dans la source (t oute cette histoire de valeur vraie doit être comprise dans le cadre d'un modèle que l'on superpose à la réalité inaccessible) Sur le plan statistique, la propriété fondamentale de la loide Poisson est  =racine(µ) Bon, il y a encore pas mal de chose à dire en partant de là, mais on va faire une pause Récré!!!Gluonmou |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Dim 11 Aoû 2019 - 19:54 Dim 11 Aoû 2019 - 19:54 | |
| Et en appuyant sur F9 vous répétez les mesures à l'infini
Ou faites 30 compteurs identiques sur 30 colonnes, vous aurez 30 valeurs d'un seul coup
Après la récré on va inverser le truc et passer aux aspects probabilistes
Là on a juste fait des statistiques |
|   | | daima
Acrobate

 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Lun 19 Aoû 2019 - 9:46 Lun 19 Aoû 2019 - 9:46 | |
| Elle dure combien de temps la récré ?  |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Lun 19 Aoû 2019 - 18:11 Lun 19 Aoû 2019 - 18:11 | |
| Ah bon? OK, s'il y a des volontaires
Je croyais que j'avais saoulé tout le monde
On va donc reprendre le chemin avec une petite question qui a l'air de rien mais qui va ouvrir de nouveaux horizons.
En résumé nous avons donc construit avec nos petits doigts une cellule qui est en soi une variable de Poisson (Siméon Denis, 1781,1840).
Cette variable aléatoire est caractérisée par un seul paramètre µ, qui peut prendre des valeurs positives quelconques (donc pas obligatoirement entières, çà l'inverse des réalisations
Lorsque vous appuyez sur F9, vous obtenez une réalisation particulière de la variable, et en répétant, vous verrez le caractère aléatoire de ces réalisations, toujours pour un même paramètre µ, que vous maitrisez (en gros vous êtes le Dieu de cette variable)
Préambule : je viens de rentrer avec mes doigts un paramètre parfaitement déterminé. Comme vous n’êtes pas derrière moi vous n'avez rien vu (je viens de vérifier, en plus c'est fastoch, je suis au bord de la mer, y'a pas grand monde, et la marée est basse (private joke valant invitation)
j'appuie sur F9, et toc j'obtient une première réalisation (comptage) égale à N1=34
Et voilà la question :
Sachant que N1= 34, A quoi peut bien être égal le paramètre µ que j'ai rentré, en cachette, et que j'ai dûment enregistré pour la postérité?
je vois des yeux qui deviennent vitreux...
Perso c'est la première question que je me suis posé à moi-même (j'aime aussi me raconter des blagues) lorsque j'ai commencé à mettre un pied là dedans
Je rend l'antenne
Gluonmou
Gluonmou |
|   | | daima
Acrobate

 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Mar 20 Aoû 2019 - 9:25 Mar 20 Aoû 2019 - 9:25 | |
| Si n est assez grand et comme l'E(N) = µ, je dirais µ= 34 (plus ou moins racine(µ) vu qu'on a fait un seul tirage). |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Mar 20 Aoû 2019 - 10:22 Mar 20 Aoû 2019 - 10:22 | |
| Je répond sans développer : non, µ n'est pas égal à 34 (en oubliant pour l'instant votre "plus ou moins racine(µ)", ça c'est une partie de la solution, il faut avant tout poser le problème)
Quel est le problème? |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Mar 20 Aoû 2019 - 12:47 Mar 20 Aoû 2019 - 12:47 | |
| Précisons :
pensez-vous pouvoir connaitre, d'une façon ou d'une autre, la valeur exacte que j'ai rentré à la main?
Si la réponse est oui, il n'y a pas de problème
Sil réponse est non, il semble y avoir un problème (dont il faut être conscient)!
Donc : oui...ou...non ?
Rayez la mention inutile
Gluonmou |
|   | | Domino
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Mar 20 Aoû 2019 - 17:45 Mar 20 Aoû 2019 - 17:45 | |
| Bonjour, ben à moins d'avoir des dons de voyance ou de trouver le coquillage sur lequel est écrit ce fameux µ. En repartant du début: j'ai un comptage unique sur un grand nombre et je peux donc appliquer la loi de Poisson. En prenant un raccourci, je me retrouve comme daima et je dis 34+/- Sauf que si je fais F9 (cher à Gluonmou) j'ai une nouvelle valeur de comptage, tout aussi valable que la précédente...et donc une autre moyenne. J'ai donc une population de de variables parmi lesquelles le 34 et une population de moyenne parmi lesquelles se trouve µ et là pour trouver µ??? 
_________________
l' ouverture d'esprit n'est pas une fracture du crâne
|
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Mar 20 Aoû 2019 - 19:00 Mar 20 Aoû 2019 - 19:00 | |
| "tout aussi valable que la précédente...et donc une autre moyenne."
Voici donc un aspect du problème
Je m'en vais essayer de l'exposer plus complètement
Accrochez-vous un peu car voici venu le moment du grand chambardement, celui de l'inversion dialectique, comme dirait Etienne Klein, ou plus précisément celui de l'inversion bayesienne. comme dise,nt les bayésiens, et pour ma part je préfère parler ici d'inversion dans ue dialectique cause-effet
Nous ne sommes plus du tout dans la situation où après avoir construit une variable aléatoire Poisonnienne dont nous maîtrisons le paramètre µ et où l'on s'amuse à faire bouger les réalisations N, qui s'empilent suivant un histogramme appelé justement loi de Poisson (de paramètre µ)
ça c'était une situation idéale, scolaire dirai-je, que l'on ne rencontre pas dans la vraie vie. Scolaire dans le sens où l'on se donne la cause : un VA de Poisson de paramètre µ (la moyenne vraie), ce qu permet d'en estimer les effets : les réalisations N
La cause précédant (préexistant les effets, comme toujours
Nous sommes maintenant dans la situation du métrologue qui , à partir d'un effet : un comptage N (lu sur un compteur), essaye d'en estimer la cause µ, cause un peu abstraite ici mais que l'on peut relier à une réalité physique : l'activité moyenne vraie contenue dans la source soumis à mesurage via le modèle d ela mesure :
Net=Rendement*Act*T
Notez que su par exemple R=1% et T = 100 s alors un comtage de 34 se traduit immdiatement par une activité de 34 Bq, ce qui est mois abstrait
Notez aussi que dans toute cette histoire nous appréhendons la réalité dans notre esprit aux travers de modèles idéaux (mathématiques) faute de ne pas être Dieu.
Ces modèles sont sous-tendus par des hypothèses, que l'on espère pas trip fausses
Et dans ce cas là en particulier l'hypothèse fondamentale que nous utilisons est de dire que la valeur de comptage
que l'on a obtenu, après peut-être 5 h de comptages (donc on ne vas pas recommencer, où pendant ce temps là on va essayer de tirer quelque chose de cette information) est une réalisation d'une VA de Poisson.
En nous appuyant sur le fait qu'en général une valeur de comptage obéit à un processus temporel de Poisson : c'est l'intégration d'impulsion (+1) bien séparées entemps, que l'on peut modéliser comme la somme de n épreuves de Bernouilli : : sur chaque durée infinitésimale dt= T/n on à une faible probabilité p d'avoir une impulsion
processus qui fabrique bien une VA de Poisson, dont nous n'avons qu'une réalisation : N1, mais pas le paramètre µ.
Notez bien là encore que cette hypothèse tient en généra assez bien la route, à condition de ne pas empiler, c'est à dire de ne pas trop charger l'activité.
Et donc notre problème est maintenant d'estimer, et estimer seulement, le paramètre µ, car il y a peu de chances (en vérité la probabilité est nulle que) que la réalisation N1 soit pile poil égale au paramètre µ.
Et même si c'était le cas (une sorte de miracle probabiliste) nous ne le saurions pas
Et de plus on sait très bien que si l'on refait d'autres comptages, nous obtiendrons des valeurs différentes l'une de l'autre. Donc ces réalisations aléatoires (qui bougent) ne permettent certainement pas de connaitre exactement la valeur du paramètre µ qui lui ne bouge pas
Nous sommes donc dans une situation d'incertitude quand à la connaissance du paramètre µ.
Et cette situation n'existe que dans notre esprit
Notez bien cela : le fait que les réalisations "bougent" pour de vrai dans le monde réel - situation de variabilité naturelle et mesurables, palpable- entraine dans notre esprit une situation d'incertitude sur le paramètre µ du modèle utilisé pour décrire cette réalité, paramètre qu n'est pas censé bouger (sinon de façon déterministe, mais c'est une autre histoire
Pour faire court : à partir d'une mesure (effet ) N1 (ou activité mesurée) nous devons estimer la cause (µ ou activité réellement contenue dans l'échantillon) mais nous savons que nous ne connaîtrons pas la valeur exacte de cette cause, sur laquelle nous avons donc une incertitude.
Ainsi la variabilité dans le monde réel entraine dans notre esprit une incertitude sur les paramètres des modèles (ou hypothèses) que nous utilisons pour décrire cette réalité.
Ouf, c'est dit
Donc surtout ne confondez pas variabilité des effets et incertitude sur les causes
Les 2 étant décrites en général avec des objets similaires : des lois de probabilité, ce qui génère souvent des confusions dommageables, que les métrologues hélas pratiquent trop souvent.
N'oubliez pas un truc : les incertitudes ne se mesurent pas, les variabilités oui
je vous laisse digérez tout cela
Nous verrons ensuite le formalisme mathématique délicat mais intuitif de l'inversion bayesienne dans le cas de notre mesure unique 34
Gluonmou |
|   | | daima
Acrobate

 |  Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire Sujet: Re: Fabriquez vous -meme votre simulateur de compteur nucléaire  Mer 21 Aoû 2019 - 15:32 Mer 21 Aoû 2019 - 15:32 | |
| Bonjour Gluonmou, je pense ne pas saisir toute la subtilité de ce que tu évoques par rapport à la différence entre variabilité et incertitudes. Pour moi il a toujours été clair que les incertitudes se calculent ou s'estiment. Et quand je donne une activité par exemple en spectrométrie gamma, je sais que la valeur donnée est une estimation de la réalité. Je ne travaille pas en métrologie, pour moi la partie mesures sert juste à estimer l'activité de colis de déchets ou d'avoir un ordre de grandeur. Aurais tu un exemple d'illustration de ta phrase ? - Citation :
- Les 2 étant décrites en général avec des objets similaires : des lois de probabilité, ce qui génère souvent des confusions dommageables, que les métrologues hélas pratiquent trop souvent.
Merci d'avance. |
|   | | | | Fabriquez vous -meme votre simulateur de compteur nucléaire |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
