|
| | Simulation la désintégration radioactive par la méthode de Monte-Carlo |  |
| | | Auteur | Message |
|---|
qwerty68
Ventriloque


 |  Sujet: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 11:04 Dim 12 Mai 2013 - 11:04 | |
| Bonjour, J'ai un projet pour le cours de «Simulation » , c'est de modéliser une chaîne de désintégration radioactive par la méthode de Monte-Carlo en utilisant la langage C. J'ai parvenu à déterminer la probabilité de désintégration d'un noyau : dN/dt=lamda*N=>dN/N=lamda*dt= probabilité de désintégration. Le résultats que j'ai obtenu est acceptable:  Mais le problème existe quand je diminue le dt jusqu'à une telle limite pour avoir un meilleur résolution. Dans ce cas là, le résultats de simulation est totalement différent en comparaison avec la loi de désintégration théorique. Est-ce que vous pouvez m'aider un peu ? Je vous remercie d'avance. Voilà ma code : - Code:
-
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
//#include "time.h"
double ur()
{
return rand()/(double)RAND_MAX;
}
main()
{
unsigned int n0=100000,nt,n02=0,nt2=0,n03=0,nt3=0,c,i,j=0;
double dt=0.1,t=0,tmax=12000,l=0.000015,l2=0.042787,x;
FILE *f;
//srand(time(0));
x=dt*l;
f=fopen("decay.txt","wt");
/*q=fopen("Br.txt","wt");
w=fopen("Se.txt","wt");*/
nt=n0;
for(t=0;t<=tmax;t+=dt)
{
j++;
for(i=0;i<=n0;i++)
{
if(ur()<x)
{nt--;
}
}
// printf("%lf",l*dt);
n0=nt;
if(j==1)
{
fprintf(f,"%lf %d\n",t,nt);
/* fprintf(q,"%lf %d\n",t,nt2);
fprintf(w,"%lf %d\n",t,n03);*/
j=0;
}
}
fclose(f);
/* fclose(q);
fclose(w);*/
printf("Voila, c'est fini !");
}
/*h(x)=((b*a*N0)/(b-a))*((1-exp(-a*x))/a-(1-exp(-b*x))/b)
g(x)=(a*N0/(b-a))*(exp(-a*x)-exp(-b*x))
f(x)=N0*exp(-a*x)
N0=1000
a=0.046834
b=0.042787*/
|
|   | | Gluonmou
Contorsionniste

 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 12:28 Dim 12 Mai 2013 - 12:28 | |
| Bonjour, Avant de regarder le code de plus près, je suppose que le point principal de votre code Monte-Carlo est le suivant, en considérant pour simplifier le noyau père : Nombre de noyaux présent à la boucle i : N(i) nombre moyen se désintégrant dNmoy=N(i) *dp avec dp=lambda.dt Comment faites-vous le tirage aléatoire pour obtenir un nombre randomisé qui doit reproduire une variable de Poisson?. pour ma part je fais une somme de N(i) épreuve de Bernouilli de paramètre dp=lambda.dt. ( soit Int (dp+rnd(1)) en VB) Si dt est très petit, vous aurez des tirage très faible (0,1,2..), avec bien sûr un grand nombre de boucle, mais ça doit marcher. J'ai fait rapidement un petit programme sous VBA, voiçi à quoi cela ressemble (toujours pour le père) Courbe 1 sur 10 période : N0=1000, T1/2=1000, dt=100, soit dp=0,067 (en rouge la courbe randomisé et en bleu en déterministe) 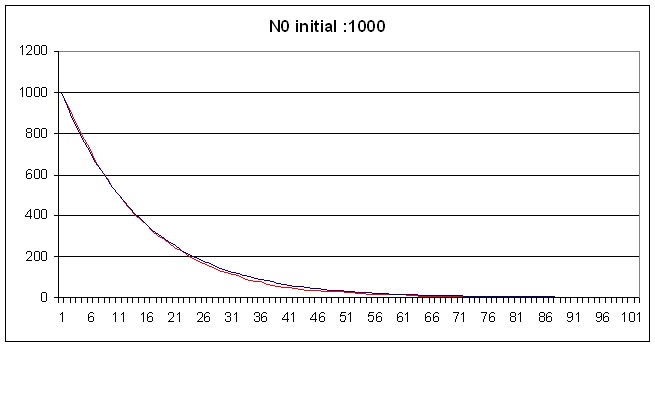 On ne voit guère de différence, l'aléa est écrasé. pour mieux le voir , on peut partir de 100 noyaux : 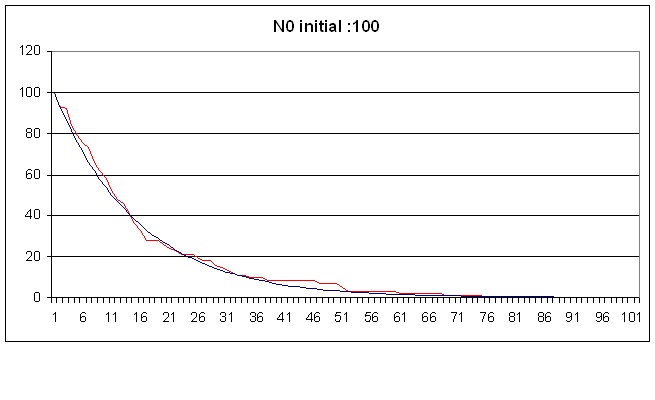 ou alors prendre 1000 noyaux et tracer la courbe sur 1 période ( N0=1000, T1/2=1000, dt=10, soit dp=0,0067) 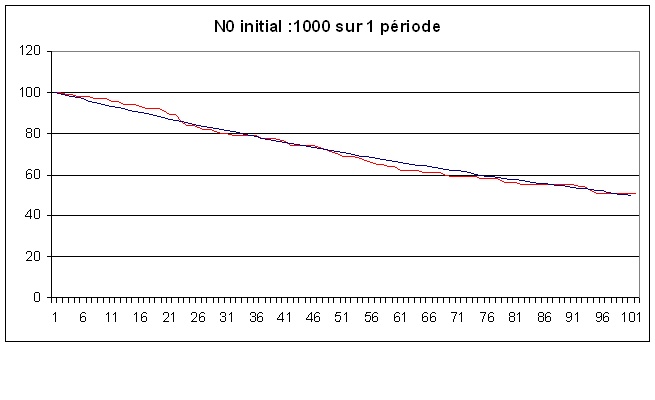 A quel niveau apparaissent vos problèmes? Je vais essayer de comprendre votre code mais je ne connais pas le langage C. Je vais mettre mon fils dessus (Son of Gluonmou) qui commence à s'intéresser à cela. Cordialement Gluonmou |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 12:48 Dim 12 Mai 2013 - 12:48 | |
| j'ai vu (gràce à Son of Gluonmou) sur votre code que vous faisiez un random entre 0 et dt. mais qu'en faites-vous après?
|
|   | | qwerty68
Ventriloque


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 14:57 Dim 12 Mai 2013 - 14:57 | |
| |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 15:18 Dim 12 Mai 2013 - 15:18 | |
| Le principe est effectivement équivalent, vous génerez une variable de Bernouilli de paramètre lambda*dt
Au niveau de la programation par contre vous générez un test à chaque fois?
Le plus simple me semble t'il est bien de générer une variable 1(succès, avec une probabilité p=lambda*dt) ou 0 (échec, avec la probabilité 1-p) et de sommer ces variables, ce qui est très proche de la réalité physique des comptages où l'on somme des pulse (+1). :
p=lambda*dt
N(t) noyaux à l'instant t
dN=0
For i=1 to N(t)
dN=dN+int(p+rnd(1)) ' (rnd(1) : random entre 0 et 1) . int : partie entière
next i
N(t+dt)=N(t) -dN
etc...
Il faut juste s'assurer que p<< 1, et normalement il n'y a aucun problème |
|   | | qwerty68
Ventriloque


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 15:27 Dim 12 Mai 2013 - 15:27 | |
| - Gluonmou a écrit:
- Le principe est effectivement équivalent, vous génerez une variable de Bernouilli de paramètre lambda*dt
Au niveau de la programation par contre vous générez un test à chaque fois?
Le plus simple me semble t'il est bien de générer une variable 1(succès, avec une probabilité p=lambda*dt) ou 0 (échec, avec la probabilité 1-p) et de sommer ces variables, ce qui est très proche de la réalité physique des comptages où l'on somme des pulse (+1). :
p=lambda*dt
N(t) noyaux à l'instant t
dN=0
For i=1 to N(t)
dN=dN+int(p+rnd(1)) ' (rnd(1) : random entre 0 et 1) . int : partie entière
next i
N(t+dt)=N(t) -dN
etc...
Il faut juste s'assurer que p<< 1, et normalement il n'y a aucun problème Puisque j'ai N noyau, c'est pourquoi je dois générer un test pour chaque noyau afin de déterminer si ce noyau se désintègre ou pas. Le problème est que le résultat se varie beaucoup quand je change un peu dt. Moi, je comprends pas encore ce point. Merci. |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 15:49 Dim 12 Mai 2013 - 15:49 | |
| Logiquement la méthode marche pour tout dt (bien sûr avec toujours la condition lambda*dt<<1)
Bien évidemment à chaque pas dt vous obtiendrez un nombre de désintégration d'autant plus petit que dt est petit, ce qui augmente le nombre de boucle si l'on veut suivre l’évolution sur une durée donnée.
Mais la simulation est d'autant plus réaliste que dt est petit (la loi de Poisson est une loi asymptotique de la loi binomiale, avec lambda*dt tendant infiniment vers 0).
Avant de faire une loi de décroissance ou d'équilibre séculaire, vous devriez vous assurer que pour un nombre de noyaux donné N0, le nombre de désintégration que vous obtenez pendant dt suit bien une loi de Poisson, et cela quelque soit la valeur de dt .Cela permettra de vous assurer que votre random et votre algorithme de base est correct |
|   | | qwerty68
Ventriloque


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 16:13 Dim 12 Mai 2013 - 16:13 | |
| - Gluonmou a écrit:
- Logiquement la méthode marche pour tout dt (bien sûr avec toujours la condition lambda*dt<<1)
Bien évidemment à chaque pas dt vous obtiendrez un nombre de désintégration d'autant plus petit que dt est petit, ce qui augmente le nombre de boucle si l'on veut suivre l’évolution sur une durée donnée.
Mais la simulation est d'autant plus réaliste que dt est petit (la loi de Poisson est une loi asymptotique de la loi binomiale, avec lambda*dt tendant infiniment vers 0).
Avant de faire une loi de décroissance ou d'équilibre séculaire, vous devriez vous assurer que pour un nombre de noyaux donné N0, le nombre de désintégration que vous obtenez pendant dt suit bien une loi de Poisson, et cela quelque soit la valeur de dt .Cela permettra de vous assurer que votre random et votre algorithme de base est correct Bonsoir, Je vous donne un calcul de moi. Avec lamda=0.000015. Je viens de faire 2 calcul avec dt=1 (ligne rouge), dt=0.5(ligne vert) et la ligne bleu est la theorie. Vous voyez, il y a un grand écart entre ces calculs qui ne devrais pas exister selon la theorie  Moi, j'utilise l'algorithme de random de la langage C.  |
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 16:27 Dim 12 Mai 2013 - 16:27 | |
| Tout cela est très bizarre.
Etes vous certain de bien ajuster l'axe des temps lorsque vous changez dt?
Pour dt =0,5 vous aurez un nombre de boucle 2 fois plus grand que dt=1, si vous voulez observer la décroissance pendant le même temps.A mon avis c'est là qu'il y a un problème
|
|   | | Gluonmou
Contorsionniste


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 16:33 Dim 12 Mai 2013 - 16:33 | |
| Faite plusieurs tirage à N0 constant, avec dt=1 puis dt=0,5
Vérifiez que pour dt donné vos tirages sont poissoniens (écartype=racine (moyenne) puis que pour dt=0,5 votre moyenne est bien la moitié que pour dt=1 |
|   | | qwerty68
Ventriloque


 |  Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo Sujet: Re: Simulation la désintégration radioactive par la méthode de Monte-Carlo  Dim 12 Mai 2013 - 16:34 Dim 12 Mai 2013 - 16:34 | |
| - Gluonmou a écrit:
- Tout cela est très bizarre.
Etes vous certain de bien ajuster l'axe des temps lorsque vous changez dt?
Pour dt =0,5 vous aurez un nombre de boucle 2 fois plus grand que dt=1, si vous voulez observer la décroissance pendant le même temps.A mon avis c'est là qu'il y a un problème
Oui, je suis sur de le faire. C'est pourquoi je ne sais pas où est l'erreur  Peut-être il y a des problèmes avec mon random. De toute façon, je vous remercie beaucoup. Désolé si mon français est mauvais car je suis Vietnamien. |
|   | | | | Simulation la désintégration radioactive par la méthode de Monte-Carlo |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
